xkcd.WTF!?

Explanation ➲

This is another comic on How to annoy people, here both graphic designers and mathematicians. This type of annoyance seems much like that displayed in 590: Papyrus and 1015: Kerning.

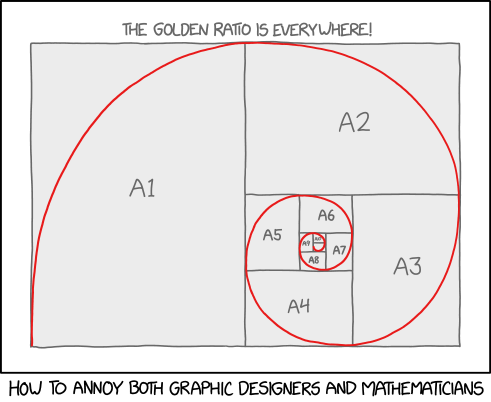
An easy way to annoy many mathematicians is to make fanciful claims about the Golden Ratio. It's been claimed, with varying levels of credibility, to be detectable in many natural and human-made situations, often with the dubious subjective claim that using the ratio in some particular way makes an image more "beautiful". The Golden Spiral is a spiral whose growth factor is this ratio; a common (though slightly geometrically inaccurate) way to illustrate the spiral is to draw curves through a set of squares whose side lengths shrink according to the Golden Ratio. The result looks rather like Randall's drawing here.

However, Randall hasn't used the Golden Ratio at all; he's just drawn a spiral (not the Golden Spiral) through a common diagram showing the A Series of standard paper sizes, but in landscape instead of portrait (this diagram is commonly drawn in portrait). These papers aren't squares at all, but rectangles whose side lengths shrink by a factor of the square root of 2. Additionally, the paper sizes shrink by a factor of one half, so the area is filled in a geometric series. This is sometimes called a silver rectangle, although the Silver ratio is actually 1+√2. By mistaking the A Series for something connected with the Golden Ratio, and perpetuating the tradition of making dubious claims about the Golden Ratio, Randall has successfully annoyed both graphic designers and mathematicians.

The title text is a similarly themed joke, based partly on the fact that the US uses customary units while the vast majority of the rest of the world uses SI units. The 11/8.5 ratio is the length/width ratio of US Letter paper, which is 11 inches by 8.5 inches (another common size in the United States is US Legal, which is 14" by 8.5"). The value of π/4 radians is indeed equal to 45 degrees, although Randall takes the cosine in one case and uses the raw angle in the other case in order to get a close coincidence of values. The width and length of A Series paper (ISO 216) is always given in whole millimeters, and the width/length ratio is very close to cos(45°) (which is 1/√2=0.707…) As for US Letter paper: to 4 decimal places, 8.5/11 = 0.7727 and π/4 = 0.7854.

In reality, the usage of radians vs. degrees is not a geographic or political decision, but generally is delineated by profession. Most engineering and science fields measure angles in degrees or fractions of degrees (arcseconds, or even milliarcseconds in fields like astronomy), while mathematicians and physicists generally use radians. Civil engineers may refer to the slope of a road by its grade, which is commonly expressed in terms of the tangent of the angle to the horizontal (either as a percentage or a ratio); for angles up to ~10°, this is close to the value of the angle in radians.

The difference between the "real" Golden Spiral squares and Randall's version is approximately either .2038 (for √2-1.6180…) or .08907 ((1/√2)-1.6180…), depending on which way you're counting. Either way, the difference would be very noticeable.

The spiral shown is approximately a logarithmic spiral with a growth factor of √2, although it has been edited slightly to make it fit neatly inside the rectangles. If the center of the spiral is at the origin, it may be graphed with r = C*2^(θ/π), for any positive constant C.

In 1488: Flowcharts a golden spiral has been laid in over the chart. That comic is a link that goes to the spiral page on xkcd.