Coffee Cup Holes
Theoretical physicist: At the Planck length, uncountably many.
Theoretical physicist: At the Planck length, uncountably many.
This comic depicts people in different fields of study answering the question, "How many holes are there in a coffee cup?" and also compares this to what a normal person would say.
This question has different interpretations, entirely dependent upon the definition of a hole. The type of coffee cup shown in the comic is with a handle (like a mug), but Randall calls it a cup and there are also cups with handles on the Wikipedia page for coffee cups. Most people would recognize that there is a hole through the handle.
The comic explores the answer to the question through several peoples’ avenues of thought, and is funny because of the ambiguity:
Topologist
Ponytail, a topologist, states the coffee cup belongs in the genus of one hole. From the topologist's point of view, the coffee cup definitely has one hole, which corresponds to the opening created by the cup handle. A cup without a handle would have zero holes, as it is equivalent to a dinner plate, just an indentation in the surface. See 2625: Field Topology for more information about topology.
The panel as a whole references an academic joke wherein topologists can't tell the difference between a coffee cup with a handle and a doughnut since they're homeomorphic to each other — meaning they have the same genus (i.e one hole).
Normal person
Hairy, representing a normal person, is not sure (the acronym "IDK" stands for "I don't know") and asks for clarification about whether the opening at the top counts as a hole. This shows flaws in the question, which suffers from the mathematically imprecise, ambiguous common usage of the word "hole." Topologists would refer to the opening as a concavity, not a hole, and while they consider such geometrical properties generally outside their field, most practical applications of topology do involve geometric components. By contrast, in everyday usage many concavities are called holes, such as a hole dug into dirt with a shovel. Hairy would say one for the handle, and two if the opening counts as a hole, which he is not certain the one asking the question thinks.
Philosopher
Hairbun, a philosopher, answers the question with an elucidating counter-question, considering a hypothetical scenario. One might expect that drilling a new hole would also increase the number of holes by one. However, as illustrated, some people would consider that the new arrangement has three holes (in addition to the handle, there is a hole at the top where coffee can be poured in, and one at the bottom where it can run out), while others would consider it to have only two (the new hole forming a continuous hole with the original opening at the top, through which coffee can run). Some might in fact say that the coffee cup now has one hole because it is leaky, disregarding the handle topology at this point. In this way she requires her interlocutor to confront the ambiguities and consider what they mean by the word 'hole' in different contexts. An interesting point about Hairbun's response is that she doesn't actually answer the question, a trope often found in philosophical replies.
Chemist
Cueball, a chemist, looks at the coffee in the cup on a molecular level. He envisions a ball-and-stick model of the caffeine molecules in the coffee, and estimates a total number of holes of all the coffee molecules. He comes up with a truly massive number: 1,000,000,000,000,000,000,000 (1021 or 1 sextillion) “in the caffeine alone.” One molecule of caffeine has two rings of bonds with holes in them, multiplied by 500 quintillion molecules, or 0.00083 moles. As the molecular mass of caffeine is about 194 grams per mole, Randall must think that the mass of caffeine in a typical cup of coffee is 161 milligrams. The coffee could have other holes, depending on the type of coffee; for example, espresso contains significant amounts of niacin and riboflavin, which have one and three rings in their chemical structure, respectively.
This estimation depends on taking the ball-and-stick model of molecules somewhat literally. However, real molecular bonds are not solid sticks, but shared electron clouds between atoms. The "holes" in the middle of a molecule's rings are not completely empty but instead merely have lower electron probability density through the middle than other parts of the bonds. So the point-cloud duality of electron orbitals and bonds might not satisfy a topologist's, normal person's, or philosopher's criteria for a connected substrate in which holes may be formed.
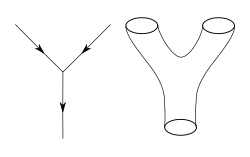String theory describes the worldlines of point-like particles as worldsheets of "closed strings," forming topological holes; shown here as a genus two surface.Theoretical physicist
In the title text, a theoretical physicist looks even deeper, at the subatomic scale of Planck units. Since fundamental particle interaction is governed by fundamental forces and collision (per the Pauli exclusion principle) instead of tensile or ductile solid connectedness, the theoretical physicist posits that any definition providing for a single hole would also describe a number of holes akin to the factorial of the number of particles in the universe,[1] or at least within the cup's light cone, which is a number impractical to accurately count, but not uncountable in a mathematical sense.
Practical considerations
The main joke is that the number of holes depends on both the scale and perspective from which you are looking at the world. From a topological standpoint, when someone digs into the ground it should go all the way through (down and up again another place) before it is considered a hole, since a hole is something that some other thing should be able to pass through. But from a common usage perspective, if people dig in the ground the result is called a hole, because functionally it creates a discontinuity in to which, for example, things can be placed or fall. Similarly, the opening in a coffee cup without a handle or a bottle of beer is called a hole, even though they are topologically equivalent to a dinner plate, which normal people would never say had a hole.
A cavity in a surface could also be considered a physical barrier, preventing movement along the surface in certain scenarios (e.g. a sinkhole opening up in the middle of a road) even though it may be topologically 'flat' in the most general way, and so is very open to context, and such a hole might be considered more a 'thing' than the surface that has been removed to create it. And a concavity in a vessel that can hold liquid (or a drilled hole which removes that ability) is of a different nature from the holes in the molecules that are part of the liquid therein. And such holes very different from the string-theoretical holes at the Planck scale, which don't necessarily involve barriers, containment, or any other aspects of topological connectivity. This conceptual ambiguity of what a hole is or means is demonstrated by the fictional portable hole, which obeys and defies a normal person's preconceptions of a hole.
The topological discussion here regarding cups and doughnuts is related to the question of how many holes there are in a human, which is excellently answered in Vsauce's video How Many Holes Does a Human Have?. This also takes a good look at the topological difference between a paper cup and a mug with handle, and how one could be morphed into a plate and the other into a doughnut.
