Solar Panel Placement
Getting the utility people to run transmission lines to Earth is expensive, but it will pay for itself in no time.

Getting the utility people to run transmission lines to Earth is expensive, but it will pay for itself in no time.
This is another one of Randall's Tips, this time a solar energy tip.
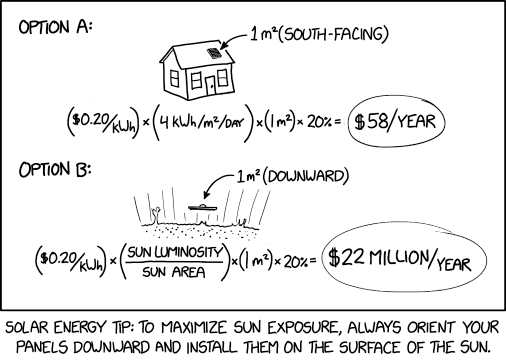
Solar panels generally produce electrical power in proportion to the intensity of sunlight striking them. In order to maximize energy production, it's generally recommended that panels be mounted at an angle that will receive the most light intensity, on average, and avoiding anything that might shade the panels. The comic might be poking fun at how sometimes solar panel arrays are installed in unusual orientations to ensure a south-facing orientation and pushing it to its logical extreme by assuming a panel on the sun.
Based on where the panel is located, the average amount of solar energy expected to strike it per day can be calculated (accounting for the angle of the sun, day and night cycles, and typical weather patterns). With this data, as well as the expected conversion efficiency and local cost of electricity, one can calculate the value of electricity the panel produces each year. In this case, Randall estimates the value of power produced by each square meter of solar cells at $58 per year.
The strip then proposes a rather intense comparison: place the identical solar panel downwards, on and towards the Sun, rather than upwards (upon a suitable equatorially-facing sloping roof), from the surface of the Earth. Due to the inverse-square law, this would result in much more solar energy striking the panel. If we assume that the solar cells could convert this energy to electricity at the same efficiency, then this would generate immense amounts of usable power, with the same calculation yielding $22 million per year as the value of a single panel in such a position.
Of course, such setup would clearly be impossible, for the simple reason that the panels would melt and then vaporize long before they reached the surface of the sun. In point of fact, current photovoltaics operate less effectively at higher temperatures, so even bringing them mildly closer to the sun would impair their efficiency, and eventually cause them to stop working altogether. This is in addition to the fact (acknowledged in the title text), that electricity produced at the sun's surface would be of little use to humans. The solution of "run[ning] transmission lines to earth" would obviously not be practical, even with millions of dollars at stake.
The assertion that the solar panel would pay for itself in no time seems flawed. For example the Helios 1 probe cost 260 million dollars in 1975 (approximately 1.5 billion dollars in 2023 money) and the Parker Solar Probe, which will fly 6.2 million km from the surface of the sun, also cost 1.5 billion dollars. The Parker Solar probe mass is 50kg, which is the same order of magnitude as a 1m² solar panel.
There are conceptual proposals, for siting solar arrays in space, but in orbit around earth, rather than than on the sun. This would allow for somewhat more solar intensity, and provide more consistent power, but the obstacles of launching the arrays into space and then transmitting the power remain serious pragmatic difficulties.
- Calculations
The formula Randall uses in this comic is electricity price × solar irradiance × panel area × panel efficiency = savings.
Electricity price is measured in dollars per kilowatt-hour, a unit commonly used by electric utility companies. In both cases, it is assumed to be $0.20 per kilowatt-hour, which is a reasonable estimate for domestic, retail electric rates in Randall's home of Massachusetts.
Solar irradiance, a special case of irradiance, is the total amount of power delivered to a surface by the Sun per unit area. This measurement varies substantially by geography, and must account for hours of daylight, angle of the sun, and weather patterns (all three of which vary by season). This number is expressed in kilowatt-hours per square meter per day, though this number is typically averaged for the whole year. Randall assumes a value of 4 kWh/m2/day, which is also reasonable for Massachusetts. He also calculates the value for the surface of the Sun as its total luminosity (electromagnetic power, ≈3.83×1026 W) divided by its total area (≈6.07×1018 m2), which comes out to around 6.31×107 W/m2 or 1.51×106 kWh/m2/day.
Solar panel area is measured in square meters.
Solar panel efficiency, a dimensionless quantity, is the fraction of solar power that a panel can effectively convert into electricity. Here, both panels are assumed to be 20% efficient, which is a reasonable estimate for commercially available photovoltaic cells operated near room temperature (300K).
Multiplying these quantities together yields a unit of money per unit time, per area (dollars per day per square meter with these specific units). For the parameters for the Earth-bound example, the formula yields $0.16 per day in effective earnings, which can be multiplied by 365 to get approximately $58 per year. For the parameters on the Sun, it instead yields $60,400 per day in earnings, or approximately $22 million per year.
It should be noted that these values are for each square meter of solar panel. Solar systems almost always consist of multiple panels. With the same assumptions, a 30-square-meter system (which is a relatively small, home system) would be worth $1,740 per year.