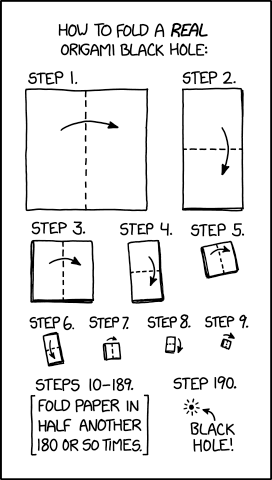
This comic shows what at first appears to be an actual page of origami directions, like this one or this one, except labeled "How to fold a real origami black hole".
The "real" part draws a contrast to an origami depiction of a black hole. A piece of origami can be made to appear like one of the various images, diagrams, or artistic depictions of a black hole. It seems black-hole-like origami does exist, as created by Richard Sweeney. The implication is that while the linked origami only resembles a black hole, Randall's instructions create an actual black hole out of origami paper.
The instructions just repeat the operation of folding the paper in half, ignoring the increases in thickness and difficulty of folding that occur. In addition, the idea that one can create a black hole with one's bare hands is far-fetched. The difficult details in actually carrying out such a thing are left implied and unexplained - and they turn out to be surprisingly complex.
The number of folds is likely based on the Schwarzschild radius of a piece of paper. The Schwarzschild radius is a characteristic of every object that depends on the object's mass. If an object is compressed into the volume of a sphere with its characteristic Schwarzschild radius, then that object will become a black hole. (More specifically, it will become a Schwarzschild black hole.) As such, if a piece of paper were folded sufficiently many times so as to fit within its own Schwarzschild radius, it would become a black hole. However, this would require compressing the paper into a flat sheet at every step, as otherwise the folded paper would double in thickness at each step, greatly exceeding its Schwarzschild radius. Indeed, it would need to be compressed beyond the thinness of the original sheet of paper.
If we assume standard kami origami paper with a side length of 15 cm and a weight of 70 grams per square meter, we get a mass of 1.575 grams, corresponding to a Schwarzschild radius of 2.339×10-30 meters. It follows that, ignoring the paper's thickness, we would need to halve each side length -log2((2 × 2.339×10-30 m)/0.15 m) = 94.69 times to fit each side length within the "Schwarzschild diameter" of the paper. Using the square folding technique in the comic, this would take 95 * 2 = 190 steps to complete, the exact number given in the comic. Note that the radius of the resulting black hole is 10-15 times the size of the charge radius of a proton. Black holes this small, if they can be created at all, are believed to quickly disintegrate by losing energy via Hawking radiation. In this case, if those predictions are correct, it would result in an energy release equivalent to 33.8 kilotons of TNT, roughly equal to two atomic bombs dropped on Hiroshima, in approximately 1.57×10-28 seconds. (This is the energy equivalent of the mass of the paper, given by E = mc2.)
In actual fact, it's not possible to fold a piece of paper this many times,[citation needed] because the amount of paper 'wasted' in each fold will quickly surpass the length and width of the paper. For an ordinary letter-sized (A4 or 8.5x11) sheet, the maximum number of folds is 7. The world record for the total number of folds of a sheet of paper is 12, done with a length of tissue paper 3/4 mile (4000 ft, 1200 m) long. A group of MIT students demonstrated 13 folds using multiple miles of paper, but had to lay separate pieces together as it made them too thick to tape them. Materials other than paper, such as thin foil, can be folded more times. Not only that but, as the title text alludes, prior to reaching any creation of a black hole, the pressures generated by the resulting fusion of its atoms must be overcome. Electron and neutron degeneracy pressure would also have to be overcome.
Naively, the instructions would produce a paper stack of shrinking area, growing in thickness exponentially. This would become impossible long before the 190 folds in half that the instructions require. In fact, with a paper thickness of around 0.1 mm, for it to be possible to fold it 190 times, the sum of the lengths and width of the paper would need to be around 10110 meters, a good 1083 times the diameter of the observable universe.
The mathematics of paper folding were augmented with work by a California high school student in 2001 who wrote equations that related the size of paper to the maximum number of folds it could make, which has not yet exceeded the low teens in human competition. This could be exceeded by scoring the paper to cut and flatten the outer layers of the folds, but its thickness would immediately surpass its length, and compressing it beyond the size of its fibers would require some way to hold it together.
Since this folded paper would typically have growing thickness, the instructions wouldn't really create a black hole unless one somehow additionally compressed the paper commensurate with its decrease in width and length. Perhaps the comic imagines the folded paper retaining the same thickness as a single sheet; then the density and pressure required would likely reach a point where fusion between hydrogen atoms begins to occur (a la the very first what if? article, Relativistic Baseball). This is later alluded to in the title text.